
One morning in 1913, Godfrey Hardy, the distinguished number theorist at Cambridge University who discovered the Hardy-Weinberg Principle, and made many contributions to the field of number theory, received a large untidy envelope adorned with Indian stamps. Inside the envelope were pages of rough notes containing weird and unfamiliar looking mathematical theorems and identities–products of the intuition of a brilliant but unschooled mind.
The originator of the letter was a poor 26-year-old clerk from Madras, India, named Srinivasa Ramanujan. So impressive was the manuscript, that Hardy made provision for Ramanujan to visit Cambridge to collaborate with him in mathematical research. In the seven years that followed, Ramanujan and Hardy established one of the most successful collaborations in the history of mathematics. In a tragic turn of events, Ramanujan contracted tuberculosis while at the peak of his creativity.
Visiting him on his death bed, Hardy opened with trivial conversation. “I drove over here to-day in a taxi with a boring number, 1729.” Ramanujan’s face brightened as though he had met an old friend, “Oh no, that’s not a boring number; it’s the smallest number that’s representable as a sum of two cubes in two different ways!”
Ramanujan’s deep intuitive understanding of numbers and their representation as infinite series spawned identities that were previously unknown to the world of mathematics. One of the remarkable infinite series he discovered for the reciprocal of pi is:
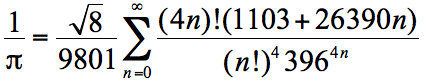
where the exclamation marks denote factorials (as well as excitement). Especially interesting is that this infinite series converges very quickly, with the first term yielding the correct value of pi to 6 decimal digits.
In 1991, American biographer Robert Kanigel celebrated the genius of Ramanujan in his award-winning book, The Man Who Knew Infinity: A Life of the Genius Ramanujan (made into a movie in 2015.) The story of a poor boy from southern India, with a modicum of formal instruction, rising to the top of the mathematical world gives us pause for thought. Does it show that genius will be served, and that environment plays a minor role in intellectual attainment? Or does it suggest that genius can come from parents of modest ability and that heredity is not a major factor in intelligence? As Haldane suggested over 80 years ago, “the task [of separating the interaction of heredity and environment] will be harder than many people believe.”
Ramanujan’s insights were fresh and uncontaminated by some of the constraints imposed by the formal approach to mathematics. Hardy, in a tribute to Ramanujan observed:
There is always more in one of Ramanujan’s formulae than meets the eye, as anyone who sets to work to verify those which look the easiest will soon discover. In some the interest lies very deep, in others comparatively near the surface; but there is not one which is not curious and entertaining.
